A Simple d12 Resolution
Wait, I thought this blog is Diceless?
Roll d12, success on 10+That’s it! Elaborations below.
Sometime during the development/Kickstarter of Knave 2e I remember Ben talked about how the default assumption of successful roll in OSR is 25%. This means rolling 16+ on a d20. The argument stems from OD&D saving throws, if I’m not mistaken.
I can see why 25% is a good cutoff for eyeballing things, but I somehow don’t like how 16 is an awkward number for a cutoff. It doesn’t feel ‘clean’, you know. No, not clean, that’s not the right word. Well I’m gonna explain it in this post, including how I arrive at d12 for the ‘cleanest’ (damn, I used that word again) die.
In a d20, there are 9 single-digit numbers and 11 double-digit numbers. Our eyes are quick to judge whether we roll 10+ or not. It’s as easy as seeing if the number shown has two digits or one. We don’t need to actually register what the number is in specific. If success is on 10+, we can just use a quick glance to know our result.
But 10+ on d20 means 55% chance of success. A slight 5% more chance of success than failure. It’s almost like coin flipping, really. If we want 25%, target number’s gotta be 16. Sadly, it imposes additional step to see the result: After determining that there are two digits, we must see if it’s 16 or higher. This means our eyes are comparing 11 numbers and must find the highest 5 numbers out of that set.
Needless to say, I won’t use d20 for this.
Roll with the Chances
Before we go much further, here is the gamefeel that I’m aiming: A quick and easy dice-based resolution.
Higher number must be better. It needs to support advantage and disadvantage without hassle. It also needs to have a static target number. And of course, a fixed target number that has a 25% chance.
Roll high is a given. It’s the most intuitive. Positive modifiers lead to positive outcome. Addition is also quicker than subtraction.
Rolling two dice, take the highest or lowest is also fun. If the default roll has two or more dice instead of one die, it teeters on the brink of hassle for me. Roll 2d6 twice, take the highest? That means rolling twice because you can’t just roll 4d6 and take the two highest. When the default is rolling one die, advantage means you just roll two of them simultaneously.
Static target number also speeds up the rolling process. No additional step of asking the GM if the roll succeeds or not. Less mental load for the GM too, since they don’t need to make up an arbitrary number each time a roll is warranted.
As for the 25%, I just like the number. It’s one of the easiest fractions. A quarter chance, 1-in-4. Most people can eyeball that chance. Having the default success rate be so low is good to me, because the characters will always have an applicable modifier or able to gain advantage. It encourages players to engage with the fiction to improve their chances.
Cloudy with a Chance of Quarter
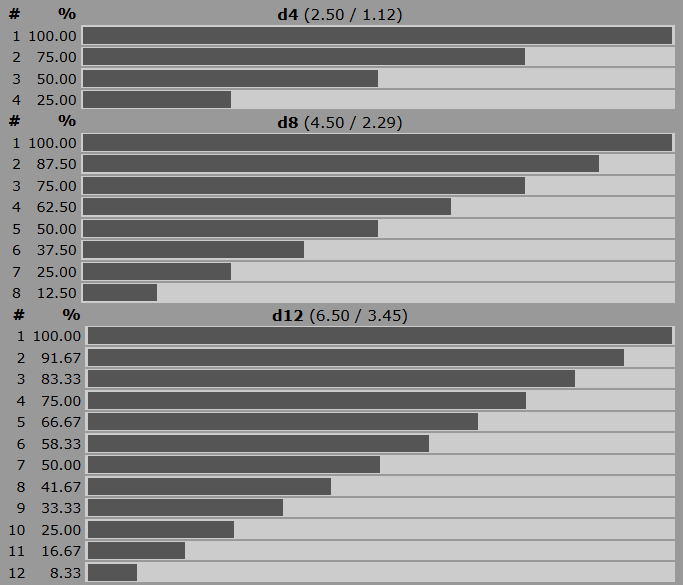
Here are the chances of rolling at least each number for d4, d8, and d12:
I only included dice that has a clear 25% chance of rolling a number, so we skip d6 and d10.
Both d4 and d8 only has single digit numbers. Maybe it’s quick to see number 4 in d4, but it doesn’t roll nice and is limited in terms of modifiers. A +1 modifier on d4 means that success is 50% already! Since I want modifiers to come from stats, and since I want stats to have potential for growth, having max stat be +2 (75% success) is suboptimal to the gamefeel that I aim.
So imagine my surprise when d12 shows that double digit numbers have 25% chance of rolling! A clear cut boundary. Roll 10 or more? That’s a success. It scales nicely too with modifiers, even in both advantage and disadvantage.
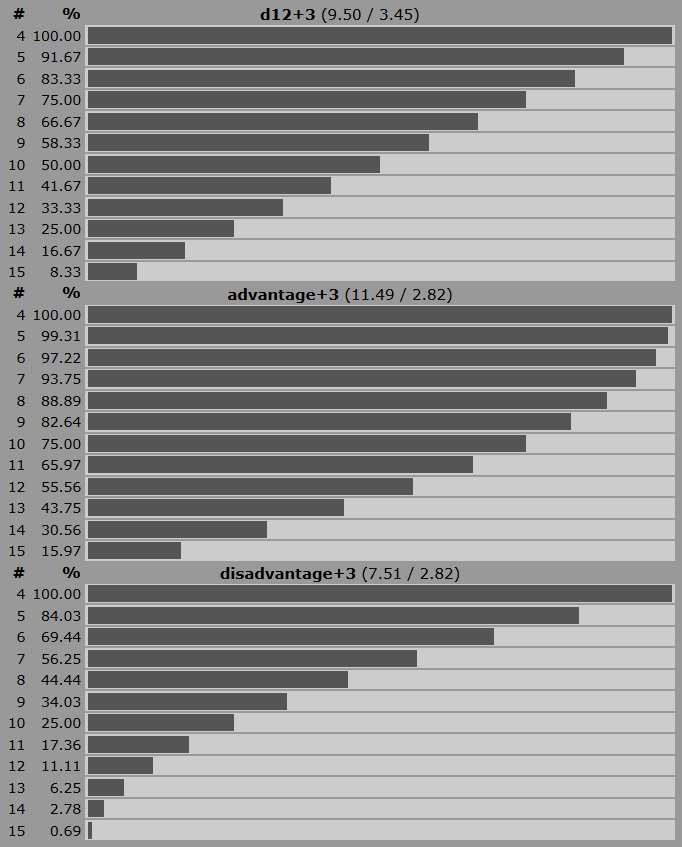
With a +3 modifier, d12 roll nets us 50% success. Advantage gives us 75%, disadvantage 25%. Neat numbers. See:
I can use 3 as the median stat value then. Maybe they’re from 0–6, since +6 nets us 75% success for a single roll, and 3 sits right in the middle of that scale.
All I Want for Crit-mas
Another problem rears its head: critical results. Natural 1 being a critical failure feels appropriate, but I don’t think natural 12 has the same oomph as natural 20. Maybe because 12 has no zeroes on it. There’s a certain decisiveness of seeing a double digit with zero that makes it natural (heh) for critical success.
In this d12 resolution, I decided to use natural 10 as the critical success. Rolling an exact number has the same chance for any number, so this is an arbitrary choice. But not so arbitrary, because I’m looking for a double digit and a zero. The number 10 feels whole. Feels suited for critical success. It might have the same feeling as playing Blackjack, what with hitting an exact specific number, no less, no more.
I think it’s neat having the cutoff target number for success be the exact number we must hit to have a critical success.
The advantage/disadvantage, modifiers, criticals are all optional rules. The core is still simple. Here it is, repeated for convenience:
Roll d12, success on 10+